Schelling Segregation Revisited

Gilad Barlev

2024-08-12

Abstract

Building on T.C. Schelling’s 1971 model of “individually motivated" racial segregation, we explore the conditions under which segregated domains coexist with integrated domains in the same system. We employ a simple agent-based model on a 2D lattice where each agent has some preference to be near other agents of like type, but which allows for random movements as well. In attempting to produce the desired results, we consider two variants: systems in which the randomness of movement varies from agent-to-agent, and systems in which an external potential is imposed on the lattice. While the first variant does not lead to the desired behavior, the second does, and we explore the effects of several several different potentials on the long-time segregation of the system.

Introduction

In 1971, T.C. Shelling introduced several dynamic models of racial segregation, showing how even the slightest preference of individuals to be near other individuals of like type could produce large-scale segregation, even in the absence of economic, legal or other global concerns. In each model, individuals of different “racial" would be placed on a lattice, and each individual would be classified as “happy" or “unhappy" based on the “racial" makeup of those around them (e.g. “happy" if 50% or more of its neighbors were of like-type). If an individual were “unhappy," it would move to a different site on the lattice. Schelling’s result was that, even if each individual had very little racial preference, segregated domains would form on the lattice. Decades later, physicists discovering the paper recognized its similarity to an Ising system and consequently suggested improvements. Noting that Schelling’s original model created segregation only on a local level and did not lead to the formation of large-scale segregated domains (a disparity that was first noticed and remedied by Jones in 1985), Stauffer & Solomon devised an equivalent $T=0$ Ising-like system, reproducing Schelling’s original results. By “increasing the temperature" (that is, increasing the probability of non-ideal moves), large domains were produced. Of course, if temperature were increased beyond some critical temperature $T_c$ , the result would be complete integration. Stauffer & Solomon interpreted this temperature as a measure of racial tolerance, and while this might make sense in explaining the phase transition between segregation and integration, this interpretation doesn’t really make sense in explaining the behavior at $T=0$ . Superficial similarities have also been noted between urban segregation and metal mixtures in binary alloys.

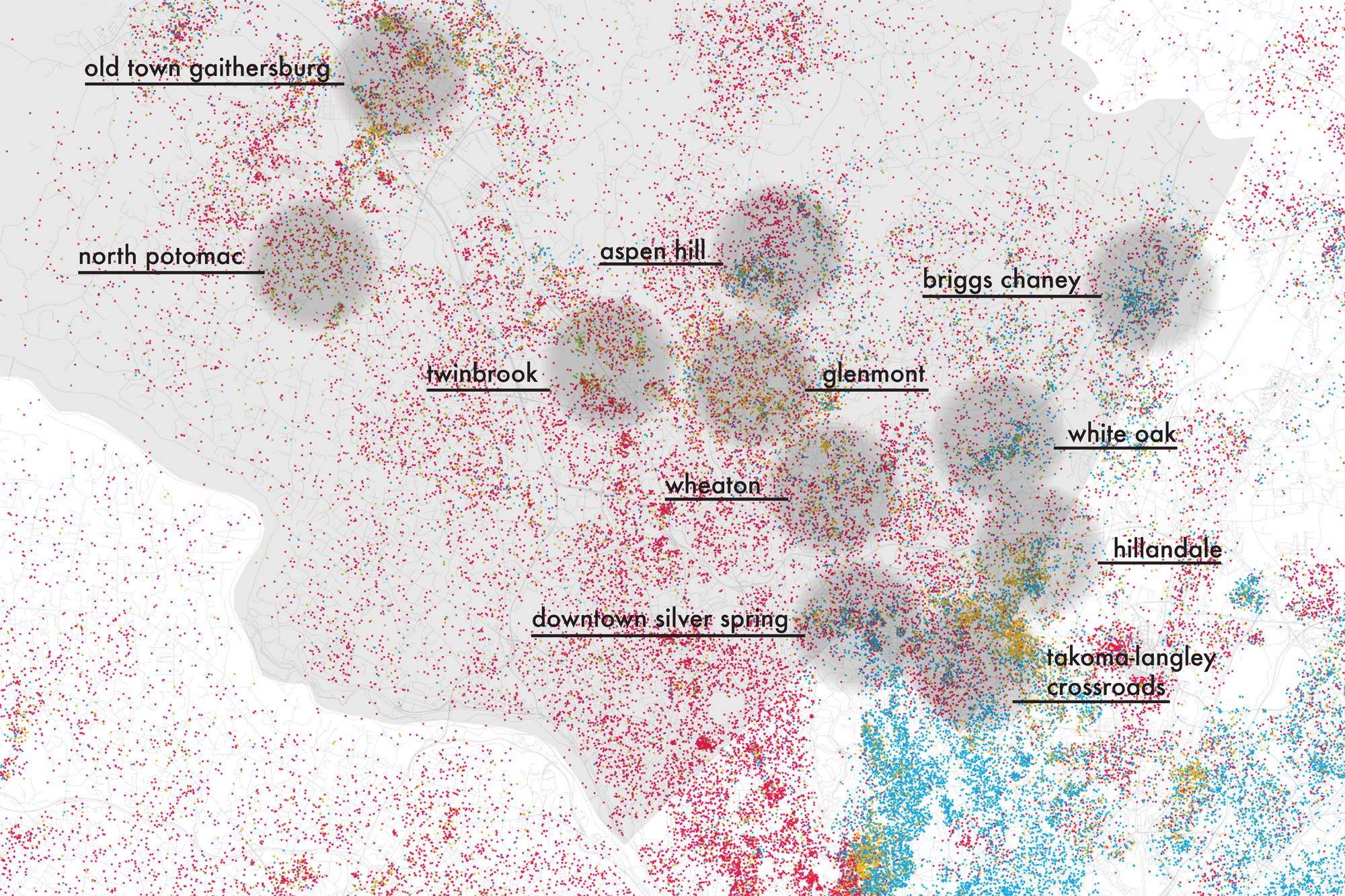
Up until this point, however, no attempts have been made to explain the phenomenon of integration and segregation existing side-by-side. Consider Fig. 1, a map of the distribution of ethnicities in Montgomery County, MD, specifically, Downtown Silver Spring and the surrounding areas. While there is a sharp ethnic divide on the East-West line to the south of Downtown Silver Spring, Downtown Silver Spring itself is heavily integrated. While it is, of course, entirely conceivable that the reason for this phenomenon could be economic (due to, say, differing property costs) or historical, this paper seeks to explore, in the words of Schelling, “individually motivated" reasons for this phenomenon, that is, a model to account for this phenomenon that can be accounted for exclusively by the decision-making processes of individuals.

Ethnicity map of Montgomery County, MD taken from 2000 US Census data. Each dot represents 25 individuals. Red represents Caucasian, Blue represents African American, Green Asian, Orange Hispanic, and Gray other. Taken from http://www.justupthepike.com/2010/09/mapping-racial-ethnic-integration-in.html.

The Basic Model

Our starting point for these investigations is based on the basic Schelling model at positive $T$ , as outlined by Stauffer & Solomon. First, we create a 2D ( $L\times L$ ) lattice and completely fill it with agents of random race. We chose to consider the case of three races (red, green and blue) at equal proportions. Then, we delete exactly one site to create a vacancy. An agent $i$ of race $R_i$ is then chosen at random. We proceed to compute its “energy" both at its current site and at the vacancy: $\label{eqn:energy}E^i(x)=\sum_{j: dist(x,j)\leq r}E_{R_iR_j}$ that is, by considering the interactions with all agents within some distance $r$ of the site $x$ .

While the matrix $\tilde E$ representing these interactions could be random, we chose to begin by exploring the simplest case: $\tilde E = \left( \begin{array}{ccc} -1 & 0.5 & 0.5 \\ 0.5 & -1 & 0.5 \\ 0.5 & 0.5 & -1\end{array}\right)$ That is, agents of like race are “attracted" while agents of differing races are “repelled."

The individual $i$ will then move to the new site if the energy difference $\Delta E^i$ between the vacancy and its current site is less than zero or otherwise with a probability $\label{eqn:move}P_{\text{move}}=\exp\left[-\dfrac{\Delta E^i}{T}\right]$ where $T$ describes a “temperature" of the system (see Section 2.1 for an interpretation of this value).

If the agent moves, it will proceed to occupy the vacancy, and its old location will become a new vacancy. If the agent does not move, another agent is selected at random. This simulates the perfect “seller’s market"–only one vacancy is ever available to be moved into at any given time, each agent has only two choices (move to that vacancy or stay where it is), and the only way for the system to advance is for someone to move to the vacancy.

To correct for certain artifacts in this method, each time a new agent needs to be selected, there is a probability $P_{OOT}$ that we fill the vacancy with a new, random individual (an “out-of-towner"). In that case, another agent is selected at random to “move out of town" and create a new vacancy.

Long-time race distributions for a simulated $200\times 200$ -site ( $L=200$ ) city with three races of approximately equal proportions. (a) At $T=0$ we see short-range segregation, but no large-scale domains form. (b) At $T=5$ large-scale segregation occurs. The picture shows the result of $1500L^2$ moves. (c) $T=15$ would appear to be above the critical temperature, leading to an integrated steady-state. $P_{OOT} = 0$ for (a) and $0.01$ for (b) and (c). The neighborhood size was set to $r=3$ . The results shown for (b) and (c) represent the culmination of $1500L^2$ moves. For (a), only $1.6L^2$ moves were performed, at which time the system ran out of viable moves.

As shown in Fig. 2, at $T=0$ (and $P_{OOT}=0$ ), Schelling’s original results are reproduced. At $0<T<T_c$ , large-scale segregated domains form, while above $T_c$ , integration dominates, agreeing with the findings of Stauffer & Solomon.

Interpretation of T

Stauffer & Solomon and others interpreted the temperature $T$ as a measure of the “tolerance" of individuals in the system, but let’s consider what changing $T$ actually does–as $T$ increases, agents in the system are more likely to move, even if it would lead them to be ethnically less “content." If these were real people, we could interpret this as meaning that these moves were performed for reasons besides ethnic similarity. In the real world, very few individuals move to a new home based solely on the ethnic makeup of their neighbors. In fact, according to the 2000 US Census, the number 2 reason for moving (behind “family reasons") was due to a new job or transfer. If someone were moving to be closer to work, they might be more likely to discount the ethnic similarity of their neighbors. So perhaps that can be our interpretation of $T$ – that societies (or individuals, as we will explore in the next section) that are more career-oriented may be modeled as having higher temperature.

Two-temperature System

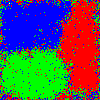
To attempt to create a system containing both integrated and segregated neighborhoods, we will begin by creating two classes of agents, each composed of equal proportions of our three races, but with class having a different temperature $T$ . So now each individual has not only a race $R_i$ but a temperature $T_i$ . Besides that, we made no changes to the model. Having set the temperature for one group well below $T_c$ and that for the other above, the result is shown in Fig. 3, and is not what we would have hoped for. Rather than segregated neighborhoods coexisting with integrated ones, what we see is segregated neighborhoods with low- $T$ cores and high- $T$ edges. This makes some intuitive sense, as high-T individuals are more willing to move into the “less desirable" locations on the borders between neighborhoods.

Long-time race (left) and temperature (right) distributions for a simulated $200\times 200$ -site ( $L=200$ ) city with three races and two temperature classes of approximately equal proportions. The temperatures of the two classes were $T=1$ (grey) and $T'=15$ (black) ( $P_{OOT} = 0.01$ , $r=3$ ). Rather than resulting in integrated and segregated domains, the system we observe shows segregated domains with mostly low- $T$ individuals at the cores and high- $T$ individuals on the edges. The distributions shown are the result of $1500L^2$ moves.

External Potential

In trying to come up with alternate methods of creating coexisting integrated and segregated neighborhoods, we considered our real-world example: Downtown Silver Spring. What if the locale itself were responsible for the integration? Specifically, what if the presence of an attraction, something that individuals of all races wanted to be near (be it a shopping center, a transportation hub, a job locus, or, as in the case of DTSS, a combination of all of the above), was enough to override the innate preference towards segregation? To investigate this, our next round of simulations included the presence of an external potential overlaid on the lattice of the following form: $\label{eqn:potential}V(x)=\left[dist(x,a)\right]^1$ where $a$ is the coordinate of the attraction. The exponent of $1$ was chosen based on the idea of commuting: if someone needs to commute to point $a$ , shaving $10$ minutes off the commute is going to be just as important if it means shortening the commute from $20$ minutes to $10$ as from $50$ minutes to $40$ . No cutoff distance was chosen for the potential–the idea is that all agents on the lattice, no matter how far out, need to commute to this attraction.

With this potential in mind, we make one small modification to our model, replacing Eqn. [eqn:energy] with the following: $\label{eqn:energy}E^i(x)=W_iV(x)+\sum_{j: dist(x,j)\leq r}E_{R_iR_j}$ where $W_i$ is a weighting term that describes just how important it is for the agent $i$ to be near the attraction.

Long-time race distribution (left) for a simulated $100\times 100$ -site ( $L=100$ ) city with three races and a site in the center imposing an attractive $r^1$ potential (right) (darker color, higher potential). The same temperature ( $T=5$ ) and weight ( $W=2$ ) values were used for all agents in the system (in addition, as before, $P_{OOT} = 0.01$ , $r=3$ ). The result is the formation of an integrated neighborhood in the vicinity of the attraction, with large segregated domains at the outskirts. The distribution shown is the result of $15000L^2$ moves (an extra long run to ensure that this was, indeed, a stable solution).

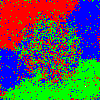
Fig. 4 shows the results of this modification. Even with all members of the population given the same weighting and the same temperature, we obtain the results we desired–around the attraction, we have dense integration, while away from it, we have large segregated domains.

This solution is interesting, as it doesn’t even come close to minimizing the energy of the system (the solution for energy minimization, by the way, is independent of the external potential, since all agents have the same weighting term). This can be explained by the fact that each agent is “greedy"–it doesn’t care about minimizing the energy of the whole system, only about minimizing its own energy. Consider an agent in the center of one of the outlying segregated regions. For the sake of argument, say all $28$ of its neighbors are of the same color. Now say it has the opportunity to move to a vacancy $22$ sites closer to the attraction. Even if none of the $28$ sites in the neighborhood of this vacancy are of the agent’s type, it will always move to this new site, even though it increases the overall energy of the system. Thus, any self-segregation that may occur near the attraction due to moves of agents already near the attraction will be undone by the influx of opportunistic agents moving near to the attraction from faraway.

Multiple Attractions

We now consider the case of multiple attractions, which can be handled in two ways. If each attractor is a necessity to all the agents in the system (for example, if one attractor is a grocery store and the other a shopping center), we can think of the potential of the system as a superposition of the potentials due to each attraction: $\label{eqn:sumV}V(x)=\sum_\alpha\left[dist(x,a_\alpha)\right]^1$

On the other hand, if both attractions serve the same purpose (for example, if both are train stations), then all an agent will care about is which attraction is closer, in other words, the potential will be determined by the minimum distance to one of the attractions: $\label{eqn:minV}V(x)=\text{min}\left\{\left[dist(x,a_\alpha)\right]^1\right\}$

Superposition

In the case of two superimposed $r^1$ potentials, the ideal location, potential-wise, will be anywhere along the line connecting the two attractions. Indeed, the combined potential in this case will be stadium-shaped, with a much larger area where the potential isn’t as steep. Consequently, one might expect our model to segregate more readily, but as Fig. 5 shows, this is not the case. Instead, the entire “low-potential" region is integrated, while the boundaries are segregated.

Long-time race distribution (left) for a simulated $200\times 200$ -site ( $L=200$ ) city with two races and two sites imposing superimposed attractive $r^1$ potentials (right) (darker color, higher potential). The same temperature ( $T=5$ ) and weight ( $W=1$ ) values were used for all agents in the system (in addition, as before, $P_{OOT} = 0.01$ , $r=3$ ). The result is still that integration dominates in the low-potential regions, while segregation is only seen in high-potential regions. The distribution shown is the result of $1000L^2$ moves.

Minimum

In the case of minimal-value potentials, we would absolutely expect a segregated solution, as each race could “lay claim" to its own attraction. Instead, as Fig. 6 shows, the result is the same as before–integration near the attractions, segregation far away, where the potential is higher.

Long-time race distribution (left) for a simulated $200\times 200$ -site ( $L=200$ ) city with two races and two sites imposing attractive $r^1$ potentials (the potential at any given site is the minimum of the potential due to each attraction) (right) (darker color, higher potential). The same temperature ( $T=5$ ) and weight ( $W=1$ ) values were used for all agents in the system (in addition, as before, $P_{OOT} = 0.01$ , $r=3$ ). The result is the formation of an integrated neighborhood in the vicinities of the attractions (the low-potential regions), with large segregated domains in the high-potential areas. The distribution shown is the result of $1500L^2$ moves.

Preliminary Conclusions & Further Investigations

In seeking to replicate the phenomenon of segregated and integrated domains coexisting in the same system, we have shown that such behavior may arise from a universal rule set, that is, it is not necessary for individuals in the system to have different decision-making processes; individuals living in integrated urban centers need not be more tolerant or cosmopolitan or career-oriented than their suburban segregated compatriots. Similarly, those choosing to live in the segregated suburbs need not be more bigoted than their integrated counterparts. Our results suggest that integration can spontaneously arise in systems just by creating destinations that appeal to all demographics. As each individual acts in their own best interests, the system as a whole diverges away from any lowest-energy (segregated) configuration.

Our model, of course, is overly simplistic–it does not take into account property costs, nor differences between individuals, be they economic or social. The “ultimate seller’s market" scheme we use may also contribute to our results, and may help explain why we do not see segregation re-emerge, even in multi-attraction systems. Further investigations would study the effect of multiple vacancies, where each agent would have a choice of where to move, beyond the choice of whether or not to move at all. We would also like to investigate more sophisticated energy matrices, that is, if the racial preferences are unequal (say, Red prefers not to be around Blues more than Blue prefers not to be around Reds, or Red prefers living near Greens than Blues).

We would also like to investigate phenomena such as repulsive potentials (say, due to a garbage dump or a high-crime area, which would probably be of a form other than $r^1$ ), potentials with hard cut-offs, and regular or irregular potential lattices. It would also be interesting to investigate real-world topologies (taking into account uninhabitable zones such as rivers, parks or dense forests). For example, the ethnic divide to the south of Downtown Silver Spring happens to fall along Rock Creek Park. We would hope that our model would reproduce such phenomena.

We allude at several points to the fact that the integrated solutions are non-ideal, energetically. It is important to point out that our simulations are all initialized to a random (integrated) configuration, far from these “ideal" configurations. Continued research would of course require some trials with the system initialized to one of these lowest-energy configurations to see whether integration arises even under those conditions, or whether the phenomena we have seen so far has merely been the suppression of the formation of segregated domains.

Finally, all the results we present here have been qualitative–we differentiate between segregation and integration based on how the system looks rather than by using any mathematical measure. For example, the total energy of the system, as defined by $\label{eqn:Etotal}E^\text{tot}=\sum_iE^i$ would no-doubt prove a useful measure, especially if we compared it to the minimum such value possible (a large departure from the minimum energy would be indicative of integration). This measure would serve as an order parameter to allow us to study phase transitions in the system with respect to the tuning parameters $T$ and $W$ , which were chosen in the above simulations strictly for the purposes of clear demonstration. This would allow for a far more rigorous treatment of the material than we have performed so far. Furthermore, we believe it might be possible to analytically derive some properties of the equilibrium conditions, for example, in the single-attractor case, the radius of the integrated neighborhood (we suspect, but have not yet attempted to verify, that this condition is that the expectation value for the energy–both potential and racial–of an agent at the edge must be equal to either the energy of the most remote agent or the average energy of all outlying agents). These types of analysis would not only strengthen our results, but our methods might prove applicable to other related systems.